Like every SNARK, in $\mathcal{P} \mathfrak{lon}\mathcal{K}$, we have to check if Gate Constraints are satisfied. Other than this, there are also Copy Constraints which have to be checked.

Consider the following Circuit & it’s trace for witness $x = 4$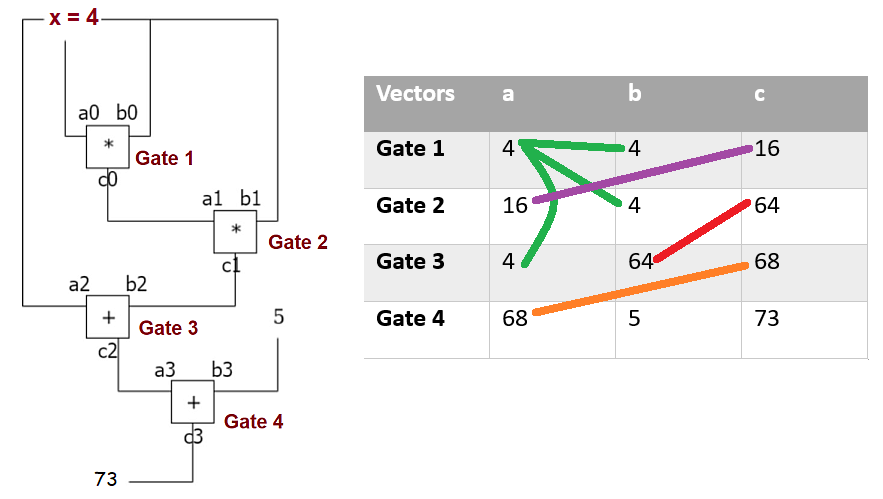

The vectors $a$, $b$ & $c$ here would be

$a = [4, 16, 4, 68]$

$b = [4,4,64,5]$

$c = [16,64,68,73]$

As shown by the coloured lines in the trace table next to circuit diagram above, we also need to check copy constraints like

• left & right input of Gate 1 have the same value

• left input of Gate 1 & right input of Gate 2 have the same value

• the output of Gate 1 is the left input of Gate 2

etc.

Checking Permutations in a vector

Let’s first consider vector $a$ alone - here we have to check that the 1st, & 3rd element are the same.

Let’s represent the permutation with a map $\sigma$

$\sigma(1) = 3$, $\sigma(2) = 2$, $\sigma(3) = 1$, $\sigma(4)= 4$

To check this, let’s create a new vector $a’$ which contains pairs, each pair containing an element of $a$ and along with its index in $a$

$a’ = [(4,1), (16,2),(4,3), (68,4)]$

We also create another vector $a’’$ with pairs, where the 2nd element of the pair is the permutation of the index of the element.

$a’’ = [(4, \sigma(1)), (16, \sigma(2), (4, \sigma(3)), (68, \sigma(4))]$

If we substitute the output of $\sigma$, this becomes

$a’’= [(4,3),(16,2), (4,1), (68,4)]$

Let’s further simplify the 2 vectors by replacing each pair $(p, q)$ with a single element $p+\beta q$ where $\beta$ is a random element selected from the operating field $\mathbb F_{97}$

So now we have the 2 vectors $a’$ & $a’’$ as

$a’ = [4 + 1\beta,\space\space 16+2\beta,\space\space 4+3\beta,\space\space 68+4\beta]$

$a’’= [4 + 3\beta,\space\space 16+ 2\beta,\space\space 4+1\beta,\space\space 68+4\beta]$

By eyeballing these 2 vectors $a’$ & $a’’$, it becomes pretty apparent that these 2 vectors contain the exact same elements, but in different order - the first element of $a’$ is the 3rd element of $a’’$ & vice versa. So now our check reduces to a check of whether $a’$ & $a’’$ are the same vector but in different order - since we have already fixed the map as part of each element, we no longer care about what order the elements are in the 2 vectors.

So how do we check if 2 sets are identical except for the order.

Let’s take a simpler example of 2 vectors $A$ & $B$.

$A = [ 2, 5, 7 ]$

$B = [ 5, 7, 2]$

We need to check if they are permutations of each other - i.e. whether both contain the same elements the same number of times even though they may be in different order.

The naive way to check would be to multiply all elements of each list & compare with product of the other.

i.e. Check if $2\cdot 5\cdot 7 \stackrel {?}{=} 5\cdot 7\cdot 2$

This will work for the above example but will show a false positive for the following pair of vectors

$A = [ 2, 5, 7 ]$

$C = [ 1, 2, 35]$

$2 \cdot 5\cdot 7 \stackrel {?}{=} 1\cdot 2 \cdot 35$ will return true even if two sets aren’t permutations of each other.

To fix this, we add a random element $\gamma \in \mathbb F_{97}$ to each element & then multiply like earlier.

So in the $A, B$ case

$(2 + \gamma)(5 + \gamma)(7 + \gamma) \stackrel {?}{=} (5 + \gamma)(7 + \gamma)(2 + \gamma)$

This will return true like it should.

In the $A, C$ case

$(2 + \gamma) (5 + \gamma) (7 +\gamma) \stackrel {?}{=} (1 + \gamma) (2 + \gamma) (35+ \gamma)$

This will return false like it should.

This simple trick of using a random number works for checking whether the 2 sets are permutations of each other.

Let’s add the random number $\gamma$ to each element our vectors $a’$ & $a’’$

$a’ = [4 + 1\beta + \gamma,\space\space 16+2\beta + \gamma,\space\space 4+3\beta + \gamma,\space\space 68+4\beta + \gamma]$

$a’’= [4 + 3\beta + \gamma,\space\space 16+ 2\beta + \gamma,\space\space 4+1\beta + \gamma,\space\space 68+4\beta + \gamma]$

Now by we can multiply all the elements of $a’$ with each other & then do the same for $a’’$ & check if the 2 products are equal

$(4 + 1\beta + \gamma)(16+2\beta + \gamma)(4+3\beta + \gamma)(68+4\beta + \gamma) \stackrel {?}{=}$

$(4 + 3\beta + \gamma)(16+ 2\beta + \gamma)(4+1\beta + \gamma)(68+4\beta + \gamma)$

Or using $\sigma$,

$(4 + 1\beta + \gamma)(16+2\beta + \gamma)(4+3\beta + \gamma)(68+4\beta + \gamma)$

$\stackrel {?}{=}(4 + \sigma(1)\beta + \gamma)(16+ \sigma(2)\beta + \gamma)(4+\sigma(3)\beta + \gamma)(68+\sigma(4)\beta + \gamma)$

This check will prove if the permutation as per the map $\sigma$ is satisfied for our vector $a$.

To simplify the above example, we used gate numbers 1, 2, 3 etc. However, as explained here, $\mathcal{P} \mathfrak{lon}\mathcal{K}$ uses elements of a multiplicative subgroup $H = \lbrace 1, \omega, \omega^2, \omega^3, …, \omega^{n-1} \rbrace$ to number the gates For the purpose of this example, we have 4 gates & so we need a multiplicative subgroup of order 4 formed by a 4th root of unity. In our toy example, we will operate in $\mathbb F_{97}$ & we can use the multiplicative subgroup generated by the 4th root of unity $\omega = 22$

i.e. $H = \lbrace 1, \omega, \omega^2, \omega^3 \rbrace$ or if we are writing values $H = \lbrace 1, 22,96,75\rbrace$.

Let’s say we have a polynomial, $a(X)$ created from the vector $a$ such that if you pass the gate number to the polynomial, it will give you value of the vector at that point. This polynomial can be created using Lagrange Interpolation. For the vector $a = [4, 16, 4, 68]$ we create the polynomial $a(X)$ by interpolating the points $[(1,4), (\omega, 16), (\omega^2, 4), (\omega^3,68)]$

$a(X) = 5x^3 + 78x^2 + 92x + 23$

So instead of the check containing elements like $4 + 1\beta + \gamma$,$16+2\beta + \gamma$ etc, we can replace the gate numbers $1, 2, 3, 4$ with $1,\omega,\omega^2, \omega^3$. We can also replace the values, $4,16$ etc with the polynomial $a(X)$ with $X$ being equal to the gate number.

So, the check for vector $a$ becomes

$(a(1) + 1\beta + \gamma)(a(\omega) +\omega\beta + \gamma)(a(\omega^2)+\omega^2\beta + \gamma)(a(\omega^3)+\omega^3\beta + \gamma)$

$\stackrel {?}{=}(a(1) + \sigma(1)\beta + \gamma)(a(\omega)+ \sigma(\omega)\beta + \gamma)(a(\omega^2)+\sigma(\omega^2)\beta + \gamma)(a(\omega^3)+\sigma(\omega^3)\beta + \gamma)$

This can also be written as

$\prod_{X \in H} a(X) + X\cdot \beta + \gamma \stackrel {?}{=} \prod_{X \in H} a(X) + \sigma(X)\cdot \beta + \gamma$

Checking Permutations across multiple vectors

The above check considers only vector $a$. However, the constraints aren’t localised to be intra vector, they actually will be inter-vector also - i.e., the output of the 1st gate (from the $c$ vector) needs to be the left input to the 3rd gate (from the $a$ vector) & so on so forth. Assuming $n$ gates, we will have a total of $3n$ elements in the 3 vectors. If we had to index $(a \cup b \cup c)$, we will need $3n$ distinct indexes So we create 2 cosets $k_1H$ & $k_2H$ each of which will be disjoint with the $n$ elements of $H$. So in $(H \cup k_1H \cup k_2H)$, we have $3n$ indexes available for the $3n$ elements. Note however that, these will only be used for indexes. For numbering gates, we need & use only the $n$ elements of $H$. We use gate numbers $1$ to $\omega^{n-1}$ for numbering the $n$ gates. Just like the polynomial $a(X)$, we also interpolate & create polynomials $b(X)$ & $c(X)$ from vectors $b$ & $c$. (Note that the $x$ co-ordinate for the interpolation for even $b$ & $c$ will only the elements of $H$ - it’s only for the $y$ co-ordinates which will use ($H\cup k_1H \cup k_2H$).

Though we had $\sigma: index(a) \mapsto index(a)$, in reality we need 3 maps $\sigma_1, \sigma_2, \sigma_3$ one each for index of elements of vectors $a$, $b$ & $c$, in each of these maps the destination could be any the index of the $3n$ elements.

The actual permutation check will be

(Perm Check)

The index numbers for Left of the Circuit would be the elements of $H$, while those for the right & output would be $k_1H$ & $k_2H$ respectively.

$\prod_{X \in H} (a(X) + X\cdot \beta + \gamma)(b(X) + X\cdot k_1\cdot \beta + \gamma)(c(X) + X\cdot k_2\cdot \beta + \gamma) \stackrel {?}{=} $

$\prod_{X \in H} (a(X) + \sigma_1(X)\cdot \beta + \gamma)(b(X) + \sigma_2(X)\cdot \beta + \gamma)(a(X) + \sigma_3(X)\cdot \beta + \gamma)$

Let’s see how to build & implement this check for our example circuit.

We have our multiplicative subgroup $H = \lbrace 1,\omega,\omega^2, \omega^3\rbrace$ with $\omega = 22$, which can also be written as $\lbrace 1, 22, 96, 75 \rbrace$

We create 2 cosets with $k_1 =2$ & $k_2 = 3$ by multiplying each element of $H$ by $k_1$ & $k_2$ respectively.

coset $k_1H = \lbrace 2, 44, 95, 53\rbrace$

coset $k_2H = \lbrace 3, 66, 94, 31 \rbrace$

As discussed earlier, we have a total of 12 elements & we will use $H’ = H \cup k_1H \cup k_2H$ to index the 12 elements

\(\begin{array} {|r|r|r|r|r|r|}\hline \qquad\qquad\qquad\quad\space &\quad\space\space \space vector\space a\quad \space\space\space& \space & \space\space\space\quad vector\space b \quad\space\space\space\space\space & \space& \quad\space\space vector\space c\space\quad\space\space\space\\ \hline \end{array}\) \(\begin{array} {|r|r|r|r|r|r|r|r|r|r|r|r|}\hline \qquad\quad\space element \space\space &a_1&a_2&a_3&a_4 & \space&b_1&b_2&b_3&b_4 & \space&c_1&c_2&c_3&c_4 \\ \hline \qquad value&4&16&4&68 & \space&4&4&64&5 & \space&16&64&68&73 \\ \hline H'\space index &1&22&96&75 & \space&2&44&95 & \space53&\space & 3&66&94&31 \\ \hline map\space\sigma &96&3&2&94 & \space& 44&1&66&53 & \space&22&95&75&31 \\ \hline \end{array}\)

In the above table, the row $H’$ index has the original index of each element (using the 3 cosets) & the map row has the mapped index for that element.

Let’s understand the map using the value $4$.

• This value appears first in vector $a_1$ (original index $1$). Since the next $4$ is at $a_3$ with index $96$, $a_1$ is mapped to $a_3$ & hence the map $sigma$ in the $a_1$ column is the index of $a_3$ which is $96$.

• The next $4$ is at $b_1$, so $a_3$ map point’s to $b_1$’s index which is $2$.

• Next is $b_2$ with index $44$ & hence $b_1$’s map points to $44$.

• That’s the last $4$ & hence $b_2$’s map points to the first $4$ ($a_1$) whose index is $1$.

So we can generate 3 maps, one each for vectors $a$,$b$ & $c$.

$\sigma_1 = \lbrace 96,3,2,94 \rbrace$

$\sigma_2 = \lbrace 44,1,66,53\rbrace$

$\sigma_3 = \lbrace 22,95,75,31\rbrace$

From these, we can use Lagrange Interpolation to compute 3 polynomials $S_{\sigma_1}$, $S_{\sigma_2}$ & $S_{\sigma_3}$

Let’s compute the polynomial $S_{\sigma_1}$ in sagemath.

Our 4 points for interpolation for $S_{\sigma_1}$ can be gathered from the above table as $[(1,96),(22,3),(96,2),(75,94)]$

If you check, each point has $x$ co-ordinate as the elements of $H$ & $y$ co-ordinate as the permuted index from $H’$. For $S_{\sigma_2}$, $S_{\sigma_3}$ also, the $x$ co-ordinate will always be 4 elements of $H$. It’s only the $y$ co-ordinate which will be one of the 12 elements of $H’$.

Let’s create $S_{\sigma_1}$ in sagemath.

(Note we are operating in the field $\mathbb F_{97}$)

sage: F97 = GF(97)
sage: R97.<x> = PolynomialRing(F97)
sage: pts = [(1,96),(22,3),(96,2),(75,94)]
sage: R97.lagrange_polynomial(pts)
8*x^3 + 73*x^2 + 39*x + 73

Likewise, we can also interpolate $S_{\sigma_2}$ & $S_{\sigma_3}$

Our Perm Check Equation

$f’(X) = (a(X) + X\cdot \beta + \gamma)(b(X) + X\cdot \beta + \gamma)(c(X) + X\cdot \beta + \gamma)$

$g’(X) = (a(X) + \sigma_1(X)\cdot \beta + \gamma)(b(X) + \sigma_2(X)\cdot \beta + \gamma)(a(X) + \sigma_3(X)\cdot \beta + \gamma)$

Let $m(X) = \frac {f’(X)}{g’(X)}$

So, what we have to check is if $\prod_{x \in H} m(X) \stackrel {?}{=} 1$

The Permutation Polynomial

Let’s define another polynomial $z(X)$ such that

• $z(\omega) = 1$ and

• $z(\omega^i) = \prod_{j=1}^{n-1} m(\omega^j)$ for $i = \lbrace 2, 3, … n \rbrace$

From the above definition

For i = 2,

$z(\omega^2) = m(\omega)$

For i = 3,

$z(\omega^3) = m(\omega)m(\omega^2)$

For i = n-1,

$z(\omega^{n-1}) = m(\omega)m(\omega^2)…m(\omega^{n-2})$

$i = n$ is the same as $i=0$ because we operating in a multiplicative subgroup of order $n$.

For i = n

$z(\omega^n) = z(1) = m(\omega)m(\omega^2)…m(\omega^{n-1})$

For i = n+1

$z(\omega^{n+1}) = z(\omega) = m(1)m(\omega)m(\omega^2)…m(\omega^{n-1})$

The above is the same as

$z(\omega) = \prod_{x \in H} M(x)$

So, we have to prove

• $z(\omega) = 1$

• We have to also prove the above steps were followed in building $z(\omega)$ - i.e., the $z$’s were accumulatively as computed above.

The Proof

Point 6 in Section 5.1 of the $\mathcal{P} \mathfrak{lon}\mathcal{K}$ Paper (Page 22) shows what needs to be done to prove this

(Note - They use $Z(a)$ while we use $z(X)$, they use $g$ where we use $\omega$ but it’s the same other than these different names.)

a) $L_1$ is $1$ at $a=1$ & $0$ at all other members of $H$ (by definition of the Lagrange Base). If at $a=\omega$, if $L_1(a)(z(a) - 1) = 0$, then it means $z(\omega) = 1$ - which if true, proves the first condition we are looking to prove.

b) As we go through 6(b) for each element $\in H$, it shows that $z$ has been built up accumulatively - i.e., each $z$ is the previous $z$ multiplied by the previous $m$.

So, proving 6a & 6b would prove our Copy Constraints.

In the $\mathcal{P} \mathfrak{lon}\mathcal{K}$ paper, this is done in Round 3 (Page 29).

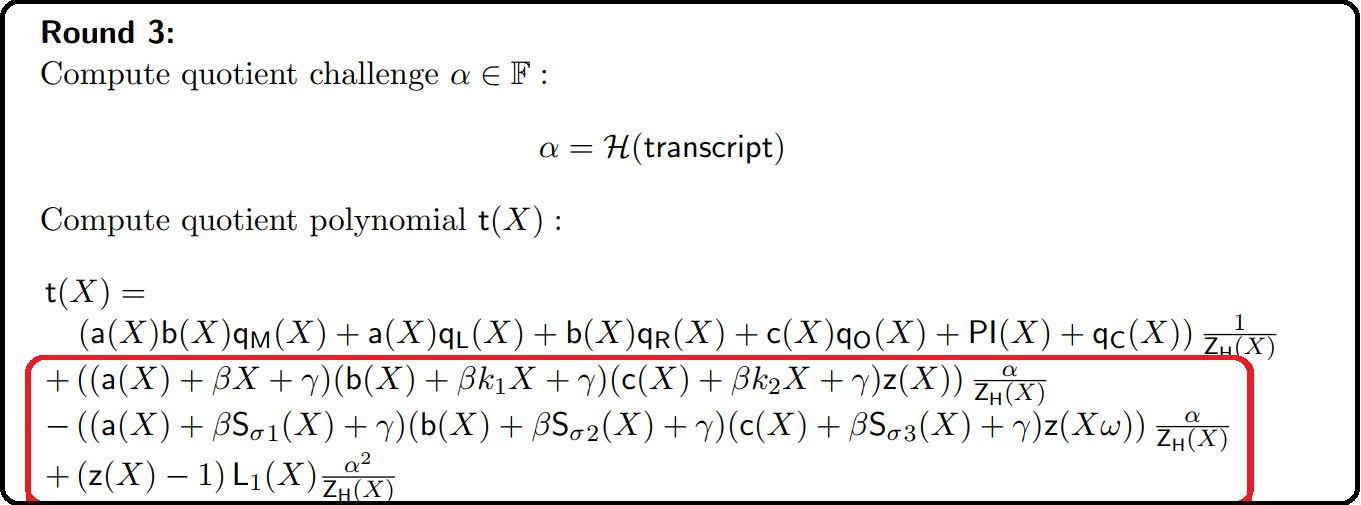
Let’s go over only the part marked in red (the others are not part of the permutation check).

The last part of the red box is

$(z(X) -1)L_1(X) \frac {\alpha^2}{z_H}$

Here $z_H$ is the vanishing polynomial i.e.

$z_H(X) = (X-1)(X-\omega)(X-\omega^2)(X-\omega^3),…,(X-\omega^{n-1})$

i.e., $z_H=0$ at every element of the set $H$ - it vanishes at every element of $H$. If a prover wants to prove that a polynomial is zero (vanishes) at every element in a set, she divides the polynomial by the vanishing polynomial for that set. Only if it divides without a remainder will the prover be able to provide a commitment to the quotient of the division. So, if the prover is able to provide a commitment to a polynomial divided by $z_H$ and is able to open the commitment successfully, then it means that polynomial is zero on every element of the set $H$.

So, if the prover is able to do this for $(z(X) -1)L_1(X) \frac {\alpha^2}{z_H}$ (we will discuss the $\alpha$ term separately), it means $(z(X) -1)L_1(X) = 0$ at all points of $H$ including at $\omega$. Which means $(z(\omega) -1) = 0$ (because $L_1(1) = 1$).

Which means $z(\omega) = 1$ which was one of the things ($6(a)$) the prover set out to prove.

Next, let’s look at first 2 polynomials inside the red box in the earlier screenshot.

If we compare it with $f’(X)$ & $g’(X)$ we defined earlier, then the 2 equations can be rewritten as

$+ (f’(X)z(X))\frac {\alpha}{z_H} $

$- (g’(X)z(X\omega))\frac {\alpha}{z_H}$

If we ignore the $\alpha$ & $z_H$ terms this is

$f’(X)z(X) - g’(X)z(X\omega)$

This is the $6(b)$ statement which the prover needs to prove. This is divided by $z_H$ for the same reason. If the provers sends a commitment to this & opens it successfully, then it means that this polynomial is zero at all points of $H$ - i.e, proof for $6(b)$. About the $\alpha$ terms in both, it is explained here. Instead proving multiple different polynomials are zero at $H$, $\mathcal{P} \mathfrak{lon}\mathcal{K}$ combines them as linearly independent terms, so it can be proven together for all those polynomials.

Round 2 Notes

Some notes about the construction of $z(X)$ which happens in Round 2 in the $\mathcal{P} \mathfrak{lon}\mathcal{K}$ Paper

Here is a screenshot of Round 2 from Page 28 of the paper

The formula for Lagrange Interpolation is

$z(X) = \sum_{i=0}^{n-1} L_i Y_i$

where $L_i(X)$ is the $i$th Lagrange base.

We have $z(\omega) = 1$

i.e., for $X=\omega$, $Y=1$

$\omega$ is the 2nd element of $H$, so $Y_1 = 1$.

We can rewrite the Lagrange interpolation as

$z(X) = L_0 Y_0 + L_1 + \sum_{i=2}^{n-1} L_i Y_i$

Again, since the last+1 element is the first element (i.e., $n$ is same as index $0$ in the subgroup), we rewrite this as

$z(X) = L_1 + \sum_{i=2}^{n} L_i Y_i$

Also, we change the $\sum$ range by using $L_{i+1}$ instead of $L_i$

$z(X) = L_1 + \sum_{i=1}^{n-1} L_{i+1} Y_{i+1}$

So that’s what is used in the screenshot above. $Y_i$ is replaced by the equation to calculate $Y_i$. The numerator of the equation is the same as the $f’(X)$ we defined earlier & the denominator is $g’(X)$

Also, the term $(b_7 X^2 + b_8 X + b_9)z_H(X)$ is added while computing $z(X)$ for blinding which is explained here

Thus, we interpolate & compute the Permutation Polynomial $z(X)$. This polynomial is then used in Round 3 as discussed earlier to create a proof for the Copy Constraints.